- 1.3 Applications Of Square Rootsmr. Mac's Page Search
- 1.3 Applications Of Square Rootsmr. Mac's Page Login
- 1.3 Applications Of Square Rootsmr. Mac's Page Sheet
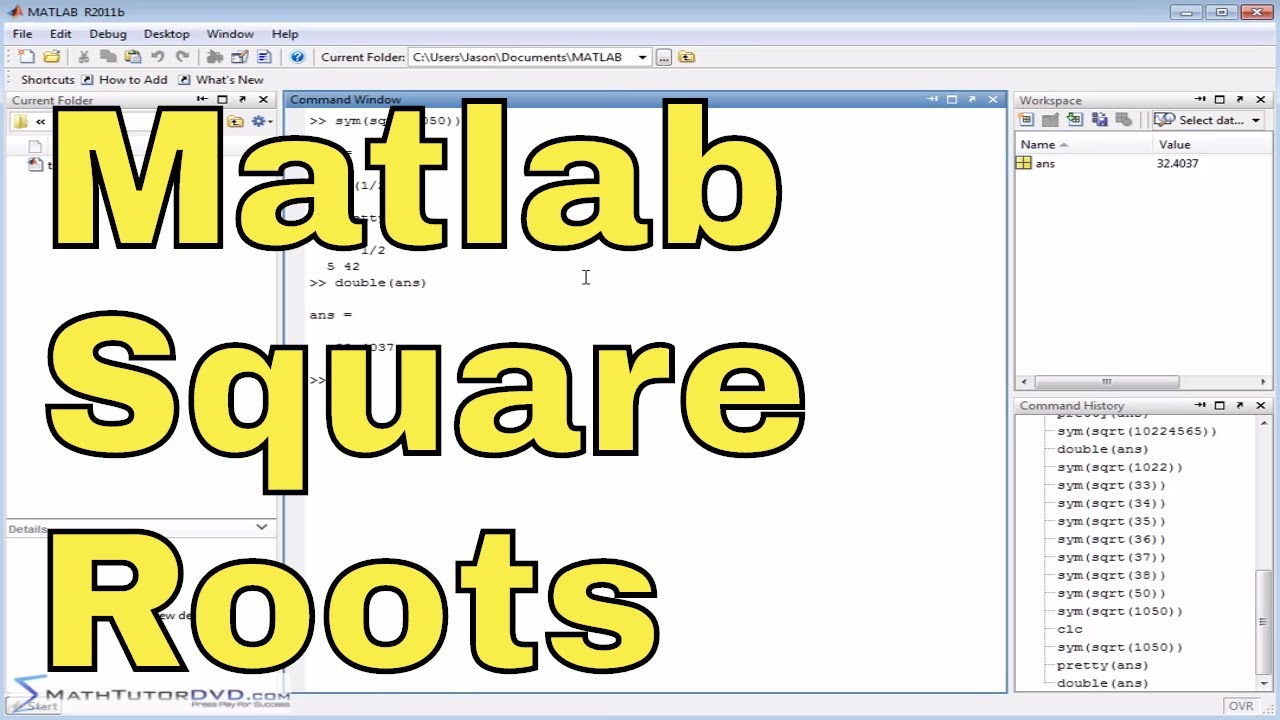
Is the number 2048 a perfect square? If not, then by which number it must be multiplied so as to get a perfect square. Find the least number that must be added to 1300 so as to get a perfect square. Also, find the square root of the perfect square so obtained. In a park there are 1225 trees. 1-3 Squares and Square Roots.3 1-4 Order of. Application files:FM:Course 2: Chapter 1 1 Course 2 Skills Practice A Plan for Problem Solving.
- Mac OS X 10.8.x, 10.9.x, 10.10.x, 10.11.x, 10.12.x, 10.13.x (Specifications are subject to change without notification, for more information please check our official website.) 1 Hig h er req uirem nts m g b needed when yo scan or edit a larg e q atity of imag d ta.
- Made from Grade 8 steel, these screws can be used in high-stress applications, such as valves, pumps, motors, and automotive suspension systems. Large flat sides make these screws easy to grip with a wrench and keep them from rotating in square holes.
We'll now turn our attention towards applying the theorem and corollary of the previous page to the case in which we have a function involving a sum of independent chi-square random variables. The following theorem is often referred to as the 'additive property of independent chi-squares.'
Theorem Section
Let (X_i) denote (n) independent random variables that follow these chi-square distributions:
- (X_1 sim chi^2(r_1))
- (X_2 sim chi^2(r_2))
- (vdots)
- (X_n sim chi^2(r_n))
Then, the sum of the random variables:
(Y=X_1+X_2+cdots+X_n)
follows a chi-square distribution with (r_1+r_2+ldots+r_n) degrees of freedom. That is:
(Ysim chi^2(r_1+r_2+cdots+r_n))
Proof
We have shown that (M_Y(t)) is the moment-generating function of a chi-square random variable with (r_1+r_2+ldots+r_n) degrees of freedom. That is:
(Ysim chi^2(r_1+r_2+cdots+r_n))as was to be shown.
Theorem Section
Let (Z_1, Z_2, ldots, Z_n) have standard normal distributions, (N(0,1)). If these random variables are independent, then:
(W=Z^2_1+Z^2_2+cdots+Z^2_n)
follows a (chi^2(n)) distribution.
Proof
Recall that if (Z_isim N(0,1)), then (Z_i^2sim chi^2(1)) for (i=1, 2, ldots, n). Then, by the additive property of independent chi-squares:
(W=Z^2_1+Z^2_2+cdots+Z^2_n sim chi^2(1+1+cdots+1)=chi^2(n))
That is, (Wsim chi^2(n)), as was to be proved.
Corollary Section
If (X_1, X_2, ldots, X_n) are independent normal random variables with different means and variances, that is:
(X_i sim N(mu_i,sigma^2_i))
for (i=1, 2, ldots, n). Then:
(W=sumlimits_{i=1}^n dfrac{(X_i-mu_i)^2}{sigma^2_i} sim chi^2(n))
Proof
Recall that:
(Z_i=dfrac{(X_i-mu_i)}{sigma_i} sim N(0,1))
Therefore:
(W=sumlimits_{i=1}^n Z^2_i=sumlimits_{i=1}^n dfrac{(X_i-mu_i)^2}{sigma^2_i} sim chi^2(n))
as was to be proved.
- Products & Services
- Enterprise Solutions
- Resource System
- Wolfram|Alpha
- Mobile Apps
- Services
- Technologies
- Solutions
- Engineering, R&D
- Finance, Statistics & Business Analysis
- Education
- Trends
- Software & Web
- Sciences
- Learning & Support
- Learning
- Need Help?
- Premium Support
- Company
- About
- Work with Us
- Initiatives
- Search
For three decades, Mathematica has defined the state of the art in technical computing—and provided the principal computation environment for millions of innovators, educators, students, and others around the world.
Widely admired for both its technical prowess and elegant ease of use, Mathematica provides a single integrated, continually expanding system that covers the breadth and depth of technical computing—and seamlessly available in the cloud through any web browser, as well as natively on all modern desktop systems.
Have a question? Contact us »
For Modern Technical Computing,
There's No Other Choice
With energetic development and consistent vision for three decades, Mathematica stands alone in a huge range of dimensions, unique in its support for today's technical computing environments and workflows.
A Vast System, All Integrated
Mathematica has nearly 5,000 built-in functions covering all areas of technical computing—all carefully integrated so they work perfectly together, and all included in the fully integrated Mathematica system.
Not Just Numbers, Not Just Math—But Everything
Building on three decades of development, Mathematica excels across all areas of technical computing—including neural networks, machine learning, image processing, geometry, data science, visualizations, and much more.
Unimaginable Algorithm Power
Mathematica builds in unprecedentedly powerful algorithms across all areas—many of them created at Wolfram using unique development methodologies and the unique capabilities of the Wolfram Language.
Higher Level Than Ever Before
Superfunctions, meta-algorithms... Mathematica provides a progressively higher-level environment in which as much as possible is automated—so you can work as efficiently as possible.
Everything Is Industrial Strength
Mathematica is built to provide industrial-strength capabilities—with robust, efficient algorithms across all areas, capable of handling large-scale problems, with parallelism, GPU computing, and more.
Powerful Ease of Use
Mathematica draws on its algorithmic power—as well as the careful design of the Wolfram Language—to create a system that's uniquely easy to use, with predictive suggestions, natural language input, and more.
Documents As Well As Code
Mathematica uses the Wolfram Notebook Interface, which allows you to organize everything you do in rich documents that include text, runnable code, dynamic graphics, user interfaces, and more.
1.3 Applications Of Square Rootsmr. Mac's Page Search
The Code Makes Sense
With its intuitive English-like function names and coherent design, the Wolfram Language is uniquely easy to read, write, and learn.
Make Your Results Look Their Best
With sophisticated computational aesthetics and award-winning design, Mathematica presents your results beautifully—instantly creating top-of-the-line interactive visualizations and publication-quality documents.
150,000+ Examples
Get started with almost any project with help from 150,000+ examples in the Documentation Center, over 10,000 open-code Demonstrations in the Wolfram Demonstrations Project—and a host of other resources.
Instant Real-World Data
Mathematica has access to the vast Wolfram Knowledgebase, which includes up-to-the-minute real-world data across thousands of domains.
Seamless Cloud Integration
Mathematica is now seamlessly integrated with the cloud—allowing sharing, cloud computing, and more in a unique and powerful hybrid cloud/desktop environment
Connected to Everything
Mathematica is built to be connected to everything: file formats (180+), other languages, Wolfram Data Drop, APIs, databases, programs, the Internet of Things, devices—and even distributed instances of itself.
Coverage
Mathematica is based on the breakthrough Wolfram Language.
The Mathematica Trajectory
It's Come a Long Way in Three Decades
The 500+ functions from Mathematica 1 are still in Mathematica 12—but there are now nearly 6,000, as well as a huge range of important new ideas that dramatically extend the vision and scope of the system.
The 1988 Revolution
When Mathematica first appeared in 1988, it revolutionized technical computing—and every year since then it's kept going, introducing new functions, new algorithms and new ideas.
Far, Far Beyond Math
Math was Mathematica's first great application area—and building on that success, Mathematica has systematically expanded into a vast range of areas, covering all forms of technical computing and beyond.
The Innovation Gets Even Faster
Mathematica has followed a remarkable trajectory of accelerating innovation for three decades—made possible at every stage by systematically building on its increasingly large capabilities so far.

Serious New Ideas in Every Version
Versions of Mathematica aren't just incremental software updates; each successive one is a serious achievement that extends the paradigm of computation in new directions and introduces important new ideas.
What You Learned in Version 1 Still Works
If you're one of the lucky people who used Mathematica 1, the code you wrote over three decades ago will still work—and you'll recognize the core ideas of Mathematica 1 in the vast system that is Mathematica today.
Always Moving Forward, for three decades
Mathematica has always stayed true to its core principles and careful design disciplines, letting it continually move forward and integrate new functionality and methodologies without ever having to backtrack.
Mathematica in the Wolfram Product Universe
Mathematica is Wolfram's original, flagship product—primarily aimed at technical computing for R&D and education. Based on the Wolfram Language, Mathematica is 100% compatible with other core Wolfram products.
Mathematica
TryBuyMathematica 12.1 is available
on Windows, macOS, Linux & Cloud. »
- Products
- Services
- For Customers
- Support
1.3 Applications Of Square Rootsmr. Mac's Page Login
- Learning
- Public Resources
- Company
- Connect
- Legal & Privacy Policy
1.3 Applications Of Square Rootsmr. Mac's Page Sheet
